Common method evaluation strategy

Visual Summary of Prediction Outcomes and Statistical Error Rates

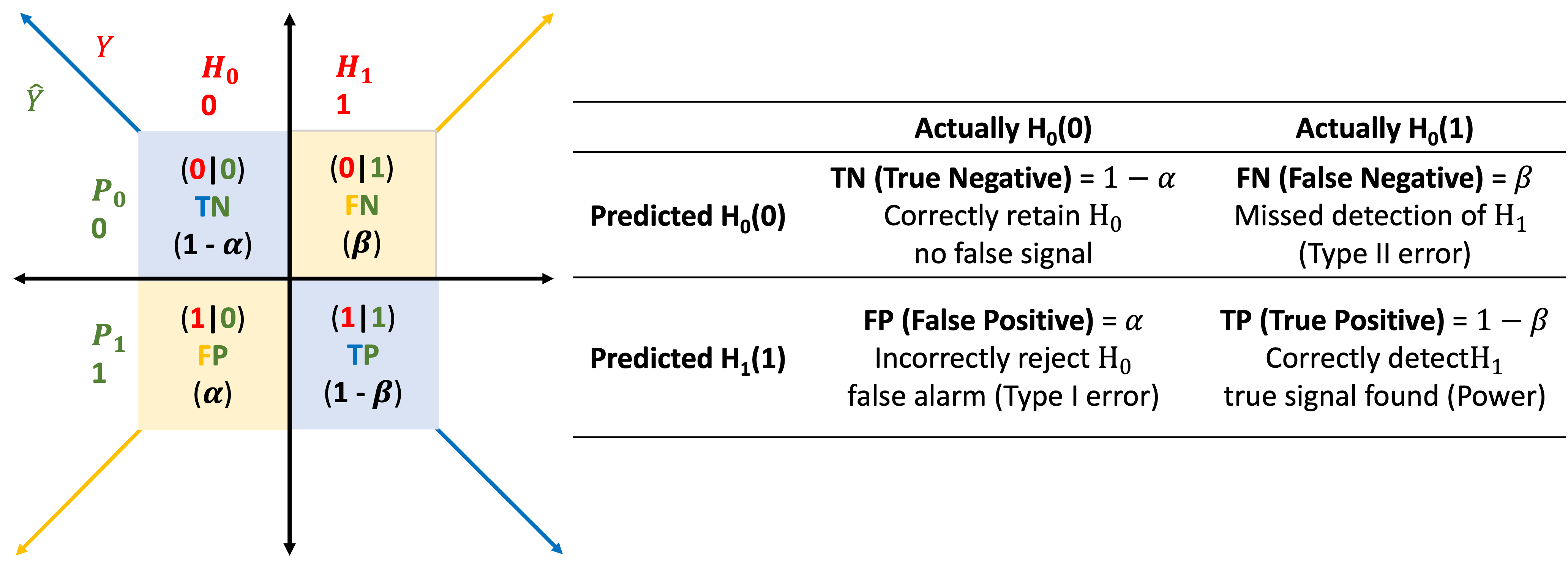
This matrix maps the relationship between predicted class \(\hat{Y}\)
and actual hypothesis \(H_0/H_1\),
with corresponding error rates and outcome labels:

• TN (True Negative): \((0|0)\) → Correct rejection of \(H_0\)

• FP (False Positive): \((1|0)\) → Type I error (\(\alpha\))

• FN (False Negative): \((0|1)\) → Type II error (\(\beta\))

• TP (True Positive): \((1|1)\) → Correct detection of \(H_1\)

Confusion Matrix Evaluation Metrics

Metric Name	Formula	Interpretation	Hypothesis Testing
1. True Positive Rate (TPR) Recall / Sensitivity	\(TPR = \frac{TP}{TP + FN}\) \(= \frac{TP}{\text{actual } H_1} = 1 - \beta\)	Probability of detecting a true alternative \((H_1)\)	Equivalent to Power
2. False Negative Rate (FNR)	\(FNR = \frac{FN}{TP + FN}\) \(= \frac{FN}{\text{actual } H_1} = \beta\)	Missed detection: actual \((H_1)\), but predicted \((H_0)\)	Type II Error Rate
3. False Positive Rate (FPR)	\(FPR = \frac{FP}{FP + TN}\) \(= \frac{FP}{\text{actual } H_0} = \alpha\)	False alarm: actual \((H_0)\), but predicted \((H_1)\)	Type I Error Rate
4. True Negative Rate (TNR) Specificity	\(TNR = \frac{TN}{TN + FP}\) \(= \frac{TN}{\text{actual } H_0} = 1 - \alpha\)	Probability of correctly retaining \((H_0)\)	Complement of Type I error
5. Precision (PPV) Positive Predictive Value	\(PPV = \frac{TP}{TP + FP}\) \(= \frac{TP}{\text{predicted } H_1} = \frac{1 - \beta}{(1 - \beta) + \alpha}\)	Among predicted \((H_1)\), how many are truly \((H_1)\)	Trust in detected signals
6. Negative Predictive Value (NPV)	\(NPV = \frac{TN}{TN + FN}\) \(= \frac{TN}{\text{predicted } H_0} = \frac{1 - \alpha}{(1 - \alpha) + \beta}\)	Among predicted \((H_0)\), how many are truly \((H_0)\)	Trust in rejected signals